- At one point I was hazy about the internal workings of leveraged and inverse ETFs, so I constructed models of hypothetical 2X and -1X Apple ETFs to clarify my understanding. I ignored a whole host of issues (e.g., regulatory, cost-effective leverage), but even a simple model of a leveraged ETF can hurt your brain. The basic inverse and leverage mechanisms shown below are essentially the same for both Exchange Traded Funds (ETFs) and Exchange Traded Notes (ETNs).
Step one: Create the “Double Apple” ETF, symbol “2AAPL”
- Complete an initial offering of 100,000 shares at $100 per share. These shares will be purchased by market makers that will manage the actual buying/selling of the 2APPL shares on the exchanges. This $10 million will provide the seed money to kick-off the ETF. This money is my initial Assets Under Management (AUM).
- Find a friendly banker with deep pockets
Step two: Put the required stock position in place
- Buy $10 million dollars of Apple stock.
- Since I’m offering 2X the performance of Apple stock I need more leverage. There are lots of ways to do this (e.g., futures, swaps), but to keep things relatively simple, I’m just buying more Apple stock
- Borrow $10 million from my banker and buy 20,000 more shares of Apple
Below I show my ETF’s first few days of operation, assuming no share creations or redemptions, with Apple stock starting at $500 per share and daily moves of +5%, +2%, -8%, +8%, and +5% over the next 5 days
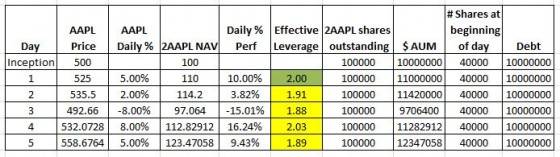
Day 1 went great. Subsequent days show my fund failing to achieve its 2X goal. What’s going on here?
The problem is that as the size (AUM) of my fund changes, I need to buy or sell Apple stock to keep my leverage at 2X.
I want my ETF to exhibit the more typical daily percentage target of 2X of the underlying security. For a 2X fund, the value of the incremental shares that need to be bought or sold in the after-market is just the percentage change in the leveraged ETF times the starting AUM. So in the example below, for day 2, my fund went up 10%, and the starting AUM was 10 million, so I need to buy an additional $1 million of AAPL stock at $525/share. These 1905 shares rebalance my fund—but I had to borrow a million dollars more from my banker to pay for them.
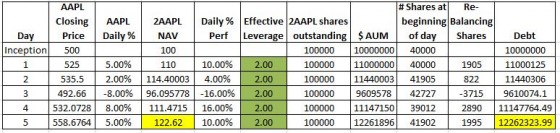
The good news is that rebalancing maintains my effective leverage at 2X. The bad news is that I have now introduced path dependency/compounding errors to my fund, and I need to borrow significant additional amounts of money.
Notice how on day 5 the 2AAPL’s NAV is 122.62 vs 123.47 on the non-rebalanced fund, and I have increased my debt by almost 25% from the inception value.
Now that I have a 2X leveraged fund working the way I want, let’s look at a -1X inverse Apple ETF. The first one does not rebalance.
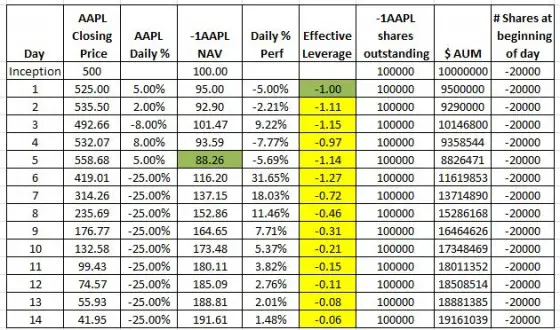
This fund will be short AAPL instead of long. Without rebalancing -1APPL will also show variable leverage. In the simulation, I added 8 days of huge drops in the price of AAPL to show one characteristic of non-rebalanced inverse ETFs.
Just like a short position, your maximum profit is limited to double your initial investment. The NAV of this fund will never exceed 200 and notice how the leverage is dropping to very low levels.
A -1X inverse Apple ETF with rebalancing is shown below:
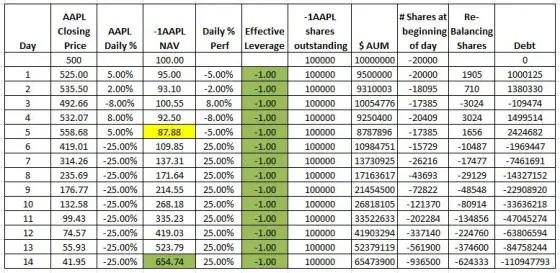
This fund exhibits a consistent -1X leverage on a daily percentage basis and doesn’t have the 100% profit limit of a non-rebalanced fund. However, like its 2X long sibling, it shows path dependencies. For example, the NAV on day 5 is lower than the non-rebalanced inverse fund.
Surprisingly the daily rebalancing required for -1X and 2X funds is identical if they have the same AUM. Notice that both rebalanced funds require +1905 shares to be added at the end of day one. For the 2X fund, the additional shares are increasing the leverage, for an inverse fund the additional shares are partially covering the short position in order to decrease the leverage.
The formula for computing the number of shares required to rebalance a constant leverage fund at the end of the day is: L * (L-1) * PercentageChange * AUMt-1 / Close. Where L is the leverage factor of the fund (e.g, -1, 2), Percentage Change is the daily % move of the underlying, AUMt-1 is the fund’s closing assets under management the previous day, and Close is the closing price of the underlying.
If inverse or leveraged ETFs are present in a thinly traded market this rebalancing process is a concern. On up days both the long leveraged and inverse funds need to buy more shares, on down days they both need to sell. If the effective market size is small these transactions could amplify market moves.

I am curious about the largest option play ever recorded this being said by Barron’s. Just a couple days ago someone guess who? Played 103,000 Contracts on UVXY The Jan 2017 Buy 9.00 Put and you can look at the volume of UVXY and verify, but what was interesting was that the article from Barron’s also stated that this was just the initial play of a much bigger play to come. I am wide open as to see where Barron’s is going with this and have sent them that with a ? behind with no response. So if anyone wants to add to what can be verified by the UVXY Play I would realy be interested in hearing. I guess that they are thinking the Markets are going to long term jump but also China and Gold will have to squeeze someone in the next couple years if Barron’s keeps hinting!
i like it. what interest are you paying on your loan from bank?
people knock double leverageds but looking at td waterhouse. it appears their margin interest rate is 7.75% and maybe higher unless you are big player. hope this isn’t completely wrong.
Hi Smc, I’m assuming I wouldn’t have to pay too much above short term treasuries, because the fees ETF’s charge aren’t high enough to cover high interest payments. The key parameter is risk–if I can convince my banker the risks are very low, then I can borrow for cheap. I could be wrong, but I think I can lay off all the risk onto the share holders–they are expecting a 2X hit if the stock goes down–so my liabilities decrease fast enough that I can offset my losses on my borrowed stock. If it doesn’t work that way then I would have to hedge my downside on the borrowed shares–put options? If Apple goes up I’m fine, the banker is only expecting their principal back with interest.
— Vance