The Sharpe Ratio
The Sharpe Ratio is one of the more popular ways to evaluate an investment for risk as well as for returns.
Assessing the risk of an investment is not easy. The Sharpe Ratio won’t protect you if the provider is dishonest (e.g., Bernie Madoff) or if historical patterns change (e.g., default rates on AAA-rated mortgage-backed securities). However the ratio does factor-in historic volatility—for example, an investment that routinely goes up and down 20% in a year will have a lower Sharpe score than a less volatile investment with the same annual returns. Volatility adds risk to an investment because the associated drawdowns might force you to take losses if you need to liquidate quickly.
Three year Sharpe ratios, as of August 2013
| SPY (div adj) | RSP (div adj) | One time random sample (normal dist) | VXX | VXZ | XIV | ZIV | |
| Ann. Monthly | 1.34 | 1.24 | -0.39 | -1.05 | -1.25 | 1.06 | 1.23 |
| Ann. Daily |
1.09 | 1.04 | -0.29 | -1.25 | -1.41 | 1.05 | 1.31 |
Oversimplifying slightly, the Sharpe Ratio divides the annualized historic returns on an investment by the annualized volatility of the investment. The annualized aspect of the Sharpe ratio is important and can lead to major errors in computing the ratio if you don’t properly account for it.
The Sharpe Ratio computation is usually computed using monthly returns and volatility—probably because it was introduced in 1966 when most people didn’t have access to computers and most calculations were done manually. Using annual returns would require multiple years of results and give pretty coarse answers and anything more frequent than monthly would have been a big computation burden.
The month based approach (as documented by Morningstar), computes the average of the monthly returns for the period of interest (this could be several years of data) and then divides that result by the volatility—which is the standard deviation of that same set of monthly returns. This intermediate result is the monthly Sharpe ratio. To convert this to an annualized Sharpe ratio we don’t multiply by 12 as you might expect, but rather the square root of 12.
Normally when we are doing time computations (e.g., months in a year), we don’t have square roots creeping into the calculation. So, why the square root?
The volatility term is the culprit—it doesn’t scale linearly with time. For example, if a market was open every day and often moved +-1% in a day, would you expect it to move +-365% in a year? No, you would expect a lot of the moves to cancel out. If the market moves are consistent with a normal (Gaussian) distribution then the expected range increases at the rate of the square root of time. For example, we would expect the weekly moves of this market to typically be 1% times sqrt(7) = +-2.64% and the cumulative move over a year to typically be 1% times sqrt(365) = +-19.1% or less. For more on this see “Volatility and the Square Root of Time“.
The Sharpe Ratio calculation multiplies the monthly returns by 12 to convert from monthly returns to year and multiplies the bottom volatility term by sqrt(12).
Since 12 / sqrt(12) = sqrt(12) the conversion of the monthly Sharpe ratio to the annualized ratio simplifies to just multiplying by the monthly Sharpe ratio by sqrt(12).
Fifty years after its introduction people are still using monthly returns for Sharpe ratio calculations—even though the daily returns (today’s price/yesterday’s price -1) of securities are readily available and spreadsheets do effortless averaging and standard deviation calculations. Calculating the Sharpe ratio using daily returns is easier than computing the monthly ratio. The average of the daily returns is divided by the sampled standard deviation of the daily returns and that result is multiplied by the square root of 252–the typical number of trading days per year in the USA markets.
Earlier I gave a slightly simplified version of the Sharpe Ratio. The real calculation subtracts the baseline return (typically USA 13 week treasury bills) from the returns before being averaged or used in the standard deviation calculation. Investors are interested in how an investment performs relative to the risk-free rate (or some other baseline index) rather than the absolute return.
This calculation is also a little tricky because compound interest is not linear with time either. The Treasury bill interest rates (e.g., ^IRX on Yahoo Finance) are usually given as an annual interest rate. Converting an annual rate to a monthly rate is not just a matter of dividing by 12. The general formula is: ((1+Annualized Return/100)^(1/Period)-1), where Annualized Return is expressed in percent, and the Period is the number of periods in a year—12 for monthly, and 252 for daily trading days.
Additional Sharpe Subtleties
The table toward the beginning of this post shows that calculating Sharpe ratios using daily returns vs. monthly returns for the same security can yield significantly different results (e.g., 20% different). I thought this might be due to the returns of the securities not being normally distributed, but when I generated returns for multiple hypothetical stocks with distributions guaranteed to be very close to the ideal I still sometimes get big variations between the daily and monthly generated Sharpe Ratios.
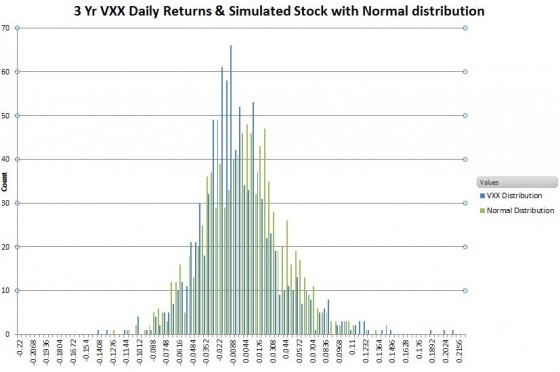
So, depending on where calendar month boundaries fall the overall volatility of returns can be emphasized—or masked. Because of this when comparing Sharpe Ratios for various investment strategies you should use the same return frequency (e.g., daily / monthly) for all of the calculations.
The Morningstar definition does not specify how dividends should be handled, I have just accounted for the cash payouts by using adjusted returns in my analysis. It would be reasonable to assume dividends were invested in Treasury bills or re-invested. The key thing is the consistency of approach between the investments you are comparing.
The Sortino Ratio
A quirk of the Sharpe Ratio is that if a security has a lot of upward jumps, which investors usually view as a good thing, it will be penalized. Any volatility, not just downside volatility increases the standard deviation and results in a decreased score. The Sortino Ratio removes this penalty by just including the downside moves in the volatility calculation. The Sortino Ratio has the same sort of time-related behaviors as the Sharpe Ratio so a calculation at the daily returns level should be multiplied by sqrt (252) to annualize it. For more on the Sortino Ratio see this article.
Three year Sortino ratios, as of August 2013
| SPY (div adj) | RSP (div adj) | Rand. (norm dist) | VXX | VXZ | XIV | ZIV | |
| Ann. Monthly | 1.11 | 0.98 | -0.47 | -1.58 | -1.75 | 0.92 | 0.88 |
| Ann. Daily |
0.98 | 0.95 | -0.29 | -1.53 | -1.66 | 0.87 | 1.15 |
I know I’ve not given enough information in this post to really compute the Sharpe or Sortino Ratio, so if you really want the details of my approach I’ve set up a free example spreadsheet here.

Thanks for the article! Just a quick question here, would it be better to use logarithmic returns when computing the sharpe-ratio given log-return is more commonly used in financial models (i.e. CAPM, Fama-French)? Thank you for your answer in advance…
Hi Caffrey, Using log returns for computing the volatility would be the standard way to compute the volatility side of things. I was following the Morningstar process when I wrote this and they didn’t specify how they computed the returns when computing the volatility. At that point I assumed they were using straight percentages.
I would expect that the impact on the results would be very slight.
Hi Caffrey, Your question has bugged me for quite a while. It turns out that the reason for using logarithmic returns is to calculate a continuously compounded return. Since Sharpe ratios are based in realized returns it’s appropriate to use percentage returns not logarithmic returns.
Thanks for the article, Vance! Sharpe Ratio has excess return in the numerator. What’s industry standard for “risk-free rate” and where can I find historical data for that?
Hi, The risk free rate is usually 13 week USA treasury bills. You can links to historical info on them n this post: https://www.sixfigureinvesting.com/2014/12/volatility-related-indexes-and-tickers/ The T-bill info is in the 3rd box from the bottom.
Hi Vance, may I know why you would multiply the avg/stdev by SQRT(252)? Have been trying to calculate my own sharpe ratios to no avail but following your instruction of multiplying by SQRT(252) actually made it seem more sound. Thanks
Hi K, The sqrt (252) takes the daily volatility number and scales it to an annualized volatility number. 252 is the typical number of trading days in a year. You might find this post https://www.sixfigureinvesting.com/2014/06/volatility-and-the-square-root-of-time/ to be helpful.
Vance
thanks for your very insightful article on Sharpe and Sortino ratios, and how to annualize from monthly or daily. The devil is in the details…