All volatility Exchange Traded Products (ETPs) use indexes that track a mix of two or more months of the CBOE’s VIX Futures. Calculating this mix is not trivial and has resulted in a lot of bleary eyes—including my own. My intent with this post is to help you understand, and if you desire to accurately compute the key indexes used in VXX and other short term volatility funds using Excel or similar tools.
Why do we need a roll anyway?
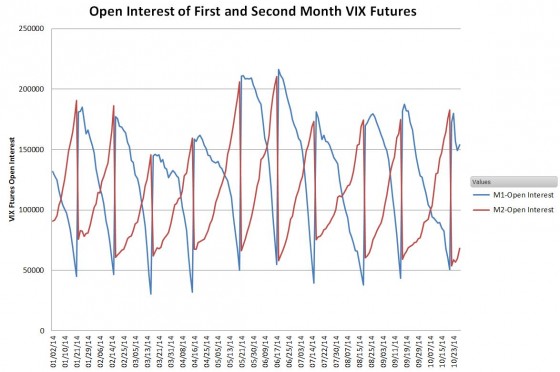
If we could directly buy the CBOE’s VIX® index none of this would be necessary. Unfortunately, no one has figured out a cost-effective approach so we are forced to use the next best thing—VIX Futures. Like options, VIX futures have fixed expiration dates so volatility indexes need a process of rotating their inventory of futures in order to have consistent exposure to volatility. This rotation process is evident in the open interest chart below—the next to expire futures being closed out and the next month of futures being opened.
Indexes and Funds—are different things
Before we dive into the details of how this rotation is dealt with, I’d like to address one source of confusion. ETP’s are not obligated to follow the approach detailed in the indexes. They are allowed to use other approaches (e.g., over-the-counter swaps) in their efforts to track their indexes. When ETPs are working properly, their prices closely track the index they specify in their prospectus minus their fees that are deducted on a daily basis.
Because indexes are theoretical constructs they can ignore some practical realities. For example, they implicitly assume fractional VIX futures contracts exist and that the next day’s position can be put in place at market close—even though calculating that position requires market close information. I’m sure these issues cause headaches for the fund managers, but to their credit, the funds usually closely track their index.
The Index Calculation
The details for the index (ticker SPVXSTR) that VXX tracks are detailed in VXX’s prospectus, pages PS-25 through PS-28. The math is general enough that it covers both the short term index that VXX uses and the midterm index VXZ uses—which adds to its complexity. The equations use Sigma notation, which probably makes it challenging for people that haven’t studied college-level mathematics. I will present the math below using high school level algebra.
Except for interest calculations, all references to days are trading days, excluding market holidays and weekends.
The volatility indexes used by short term volatility ETPs (list of all USA volatility ETPs) utilize the same roll algorithm—at the end of each trading day they systematically reduce the portion of the overall portfolio allocated to the nearest to expiration contracts (which I call M1) and increase the number of the next month’s contracts (M2).
The mix percentages are set by the number of trading days remaining on the M1 contract and the total number of days the current M1 will be the next to expire contract (varies between 16 and 25 days). So if there are 10 days before expiration of the M1 contract out of a total of 21 the mix ratio for M1 will be 10/21 and 11/21 for M2. At close the Tuesday before the Wednesday morning M1 expiration there’s no mix because 100% of the portfolio is invested in M2 contracts.
It’s important to understand that the mix is managed as a portfolio dollar value, not by the number of futures contracts. For example, assume the value at market close of a VIX futures portfolio was $2,020,000, and it was composed of 75 M1 contracts valued at 12 and 80 M2 contracts at 14 (VIX futures contracts have a notional value of $1K times the trading value). To shift that portfolio to a 9/21 mix for M1 and 12/21 for M2 you should take the entire value of the portfolio and multiply it by 9/21 to get the new dollar allocation for M1, $865,714 (72.14 contracts) and 12/21 times the entire portfolio value to get the dollar allocation for M2, $1,154,286 (82.45 contracts).
Value weighting gives the index a consistent volatility horizon (e.g., 30 calendar days)—otherwise higher valued futures would be disproportionately weighted.
The next section is for people that want to compute the index themselves. Yes, there are people that do that. If you are interested in the supposed “buy high, sell low” theory of roll loss you should check out the “Contango Losses” topic at the bottom of this post.
The Variables
Lowercase “t” stands for the current trading day, “t-1” stands for the previous trading day.
The index level for today ( IndexTRt ) is equal to yesterday’s index (IndexTRt-1) multiplied by a one plus a complex ratio plus the Treasury Bill Return TBRt. The index creators arbitrarily set the starting value of the index to be 100,000 on December 20th, 2005.
The number of trading days remaining on the M1 contract is designated by “dr”. The “dt” is the total number of trading days that the M1 contracts are the next to expire futures contract.
M1 and M2 are the daily mark-to-market settlement values, not the close values of the VIX futures. The CBOE provides historical data on VIX futures back to 2013 here.
The Equations
When dr is not equal to dt:
When dr = dt (the day the previous M1 expires) we have a different equation:
Yes, this 2nd equation could be simplified because dr/dt = 1, but then it wouldn’t fit as nicely into the equation below which uses a little logic to combine both cases:
The equation assumes that the entire index value is invested in treasury bills.
Contango Losses
- An interesting special case occurs when you assume that the M1 and M2 prices are completely stable and in a contango term structure for multiple days—for example, M1 at 17 and M2 at 18. In that situation, the equation simplifies to:
- This special case illustrates that there is no erosion of the index value just because it’s selling lower price futures and buying higher-priced futures—in fact, it goes up because of T-bill interest. It’s the equivalent of exchanging two nickels for a dime—no money is lost. For more on this see: The Cost of Contango.
For more information:

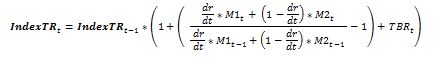
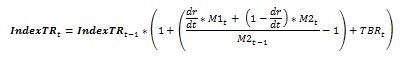
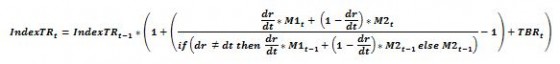
Hi Vance,
Congratulations on the excellent blog posts!
Since VXX is an ETN and VIXY is an ETF, how come VXX has so much more trading volume than VIXY? They are both designed to track the front end of the futures curve. Thanks.
Hi Pdp,
Thank!
Regarding VXX vs VIXY, I think one reason is because VXX’s tax treatment is like a stock, being reported on the IRS 1099 form. Since VIXY holds VIX futures directly their tax treatment involves K-1 forms, which isn’t a big deal but definitely adds some complexity at tax time. A second factor might be the maturity of VXX’s option market, it has a lot more volume than VIXY’s options. A third factor, which I doubt people are aware of, but VIXY cost structure is a bit more expensive than VXX. As an ETN VXX tracks its index, SPVXSTR, whereas as an ETF VIXY tracks the value of the assets it holds–as a result trading costs in VIXY get passed on to the shareholder in VIXY, but not in VXX.
Vance
Hi Vance,
Based on the VXX prospectus, the mix is managed as of number of contracts instead of portfolio dollar value. You could verify this by
( http://www.ipathetn.com/US/16/en/details.app?instrumentId=259118 )
Using the market Capitalization times index component ratio then divided by VIX future settlement price .
Hi Yongjie, I disagree. The index component number you reference does map directly into contracts but the index component value used includes the price weighted value of the futures along with the the target roll ration.
Vance
Vance, given the announcement by the OCC regarding the Note of VXX coming to maturity in Jan 2019, what do you believe Barclays will do with this product. Will they issue a new note and proceed or will it be terminated and cease trading? PA
Hi Vance,
Isn’t VIX a measure of Volatility? Then shouldn’t we square it up to get Variance which is additive/linear in time, and then use the result to calculate the Volatility? Why are we directly time-weighting the VIX?
Thanks,
Hi Ankit, Not sure I understand your question. In the case of this post we aren’t trying to calculate volatility, the equations are for computing the index that VXX tracks. Of course volatility impacts the VIX futures that ultimately determine the index values, but the futures usually seriously lag the VIX. If we were trying to compute a volatility number based on the M1 & M2 values then you are correct, converting to variance and then linearly interpolating/ extrapolating would be the correct approach. The actual VIX calculation does that with SPX option implied volatility numbers. https://www.sixfigureinvesting.com/2014/10/calculating-the-new-vix-easy-part/
Vance
Hi Vance, Thanks for your reply. I understand the methodology for calculating the VIX no, [ i.e. summing up the Puts and calls prices weighted by the inverse of the squares of strikes], this methodology gives a variance no and the square root of which would provide the resulting VIX no.
Without getting any further technical detials, since we know Variance (and not Vol) is linear and additive in time, shouldn’t the variance be used to rebalance the VXX ETFs (i.e. squares of the M1 and M2 numbers), or am I wrong when the methodology is time-weighted average of the two VIX futures numbers.
Hi Ankit, If the goal was to calculate a volatility measure then I would agree, but in reality they just wanted a roll algorithm that was relatively easy to implement. In practice the term structure curve between M1 and M2 is relatively straight, and until Weekly VIX futures started trading there were times when the closest to expiration future had 35 days until expiration–so achieving an exact 30 day volatility horizon would be tough.
Best Regards,
Vance
I don’t want to sound stupid but i don’t get why the mix ratio for M2 is 11/21?
In the example, the M1 contract is the front month for a total of 21 trading days. Let’s say it’s a May Futures contract, which would expire in May. The 21 is the number of trading days from when the previous front month (April) contract expired until this contract (May) expires. On the day the April contract expired all the contracts were held in May futures. On that day the May futures switch from being M2 contracts to being M1 contracts.
The roll then moves contracts from the front month (M1) (May) to the second month (M2) (June) over the course of time the May future is the front month. If there are 10 trading days left in the May future then the roll algorithm calls for 10/21 of the dollar value of the M1 + M2 position to be allocated to the M1 (May) futures and the remainder, 11/21 to be allocated to the M2 (June) future. For each trading day the two fractions ( in this case 10/21 and 11/21), must always add up to one.
Dear Vance, please explain me the 2nd equation where dr = dt. When I use some algebra on the first equation with dr = dt, I get a different equation. Thank you.
The language in this article is a bit misleading. The second equation with dr=dt is not a simplification of the first equation. It’s a special case when the second month contract (M2) rolls into and becomes the front month (M1). For this case, M2_t-1 is the same contract and prior day price of M1_t. M2 of day t-1 becomes the front month M1 on day t.
I modified the post a bit to make it clearer what equation could be simplified. Thanks.
Hi Vance – Thanks for responding to my earlier question about the weights used for daily calculations, and sharing this link. I was trying to follow your analysis and wanted to point out a couple of things:
1. I was trying to understand the statement: “The mix percentages are set by the number of trading days remaining on the M1 contract and the total number of days it’s the next to expire contract (varies between 16 and 25 days)”. Is there a typo somewhere in the statement?
2. In your numerical example for a portfolio that begins with a total value of $2,020,000: If it has 75 M1 contracts valued at 12, that’s a total M1 value of 12*1000*75=$900,000. However, using an allocation ratio of 10/21, I get (10/21)*$2,020,000=$961,905. I used 10/21 since you talk about shifting the portfolio to 9/21 subsequently. How do I reconcile the $900,000 and $961,905?
As always, thanks for taking the time. much appreciated.
Hi rrtrader,
Your point 1 is a typo. Should be “in” not “It’s” . Thanks! Fixed.
Point 2: The $2,020,000 was the close value for the day, the allocation shift to prepare for the next day should be 9/21 dollars for M1 contracts and 12/21 dollars for m2 contracts.
The 10/21 ratio would have been applied to the portfolio value at the close of the previous day to set the number of m1 contracts–the value of the M1 contracts after rolling the previous day is indeterminate in this example because I didn’t provide the closing value of the M1 contract for the previous day.
Vance – good article, well done. Seems to me that the vxx is doomed to a slow bleed regardless of market conditions. It’s been a long term short of mine. I considered increasing short exposure further, but I’m slightly worried about what risk there is in the upward direction. Would that risk amount to just sitting through an extended period of increased iVol until it normalizes again, or do you see other risks in the model that should be considered?
Again, I’m short the vxx. My thesis is simple: roll cost will always mean slow decay. As long as the rate of decay outweighs borrow costs, then the primary risk is an extended period of elevated iVol. You agree? Or am I missing something…
My post https://www.sixfigureinvesting.com/2016/10/is-shorting-uvxy-tvix-vxx-the-perfect-trade/ goes into the downsides/risks of this trade. A long bear market is your biggest risk. I don’t see a scenario where the iVol doesn’t eventual return to contango conditions and continue grinding VXX towards zero.
much appreciated. another well written article vance, you’re good at laying things out simply.
my view is similar, i’m struggling to find a scenario where a short position in the vxx won’t eventually be profitable.
iVol is already a mathematical fixing…the vix is a basket of those fixings…add futures on top and then another basket, and you’re four times removed from anything real.
as well as an outright short, i find it’s also a good way to hedge an options portfolio. if you end up buying protection when iVol is high, shorting the vxx along with it is a reasonable way to counter a vol compression. i got tired of buying a series of puts only to watch them lose a third of their value overnight as vol eases.
you a risk guy or pm?
Not sure I completely agree with point 1. dt is the number of business days for M1 to mature on roll day when M1 has 100% weighting and dt remains fixed until the next roll date.
Similarly defining dt as “the total number of trading days on the M1 contract” is misleading as that would be several months for any contract.
I changed the language slightly to hopefully make this clearer. Thanks. .